Giới thiệu
Trong thời gian học Đại học của mình, chương trình học có một môn học tên là Regression Analysis. Tên rất kêu nhưng giáo viên dạy môn học này của mình rất qua loa và không chú ý đến chi tiết của các định lí. Vậy nên, lần này, mình sẽ viết góc nhìn xác suất của các thuật toán hồi qui tuyến tính nhằm chỉ ra rằng việc sử dụng các thuật toán tối ưu hoá là chưa đủ để có thể tạo ra các mô hình học máy hoàn chỉnh. Bài viết này mình chia thành 3 phần: Phần 1 là động cơ để mình viết bài blog này, phần 2 mình sẽ giới thiệu sơ về thuật toán hồi qui tuyến tính, phần 3 sẽ là về góc nhìn xác suất của thuật toán và làm sao để sử dụng thuật toán này với hiệu quả cao nhất và phần cuối cùng sẽ là kết luận bao gồm một số nhược điểm của thuật toán này.
Thuật toán hồi qui tuyến tính (Linear Regression)
Có thể nói, thuật toán hồi qui tuyến tính là một trong những thuật toán cơ bản nhất trong tất cả các thuật toán học máy sử dụng tham số có giám sát (là các thuật toán xây dựng mô hình học máy bằng các giả định về mối quan hệ giữa nhãn (label) và các thuộc tính (attributes)). Ngay cả các thuật toán mạng nơ-ron (neural network) cũng được xây dựng từ thuật toán này mà ra. Vậy nên, hiểu được cách vận hành của thuật toán này sẽ giúp bạn cảm thấy dễ hiểu các thuật toán máy học cao hơn.
Thuật toán hồi qui tuyến tính như tên gọi xây dựng dựa trên giả định rằng nhãn có mối quan hệ tuyến tính với các thuộc tính. Phát biểu một cách toán học thì nếu gọi $y$ là biến cần dự đoán (ví dụ như giá nhà chẳng hạn) và $x_1$, $x_2$, $\ldots$, $x_n$ là các thuộc tính mà có thể biến $y$ sẽ phụ thuộc vào (như giá nhà thì phụ thuộc vào số phòng của ngôi nhà, nhà cao bao nhiêu tầng, diện tích nhà rộng không, nhà có bao nhiêu mặt tiền, vân vân) thì thuật toán hồi qui tuyến tính giả sử rằng tồn tại các tham số $w_0$, $w_1$, $\ldots$, $w_n$ sao cho
\[\begin{align*} \widehat{y} = w_0 + w_1x_1 + w_2x_2 + \ldots + w_nx_n. \end{align*}\]Trong giới khoa học, một bộ $(w_0, w_1, \ldots, w_n)$ được gọi là một bộ trọng số. Mục đích của thuật toán hồi qui tuyến tính là để tìm ra bộ trọng số tối ưu để ước lượng mối quan hệ tuyến tính giữa nhãn và thuộc tính dựa trên một tập dữ liệu có sẵn. Nhưng khi đã dùng đến từ tối ưu thì phải có một “tiêu chí” để đánh giá xem bộ trọng số nào tối ưu hơn bộ trọng số nào. Và “tiêu chí” đó chính là hàm mean-squared error để tính sai số giữa dự đoán của mô hình ($\widehat{y}$) và nhãn ($y$).
\[J(w_1, w_2, \ldots, w_n) = \dfrac{1}{m}\sum_{i=1}^m\left(y_i - \widehat{y}_i\right)^2\]Giả sử ta có một tập dữ liệu $\mathcal{D} = \{(x_{i, 1}, x_{i, 2}, \ldots, x_{i, n}, y_i)|i=\overline{1,m}\}$ với $x_{i, j}$ là giá trị ở thuộc tính $j$ của ví dụ $i$ và $y_i$ chính là nhãn tương ứng. Với mỗi bộ trọng số $(w_1, w_2, \ldots, w_n)\in\mathbb{R}^n$ thì hàm mean-squared error ứng với bộ tham số đó được định nghĩa:
với $\widehat{y}_i = w_0 + w_{1,i}+ w_2x_{2, i} + \ldots + w_nx_{n, i} $.
Có thể nhìn thấy mean-squared error có hơi hướng giống với khoảng cách giữa 2 điểm trên hệ toạ độ Decartes n chiều. Như vậy, rõ ràng bộ trọng số càng tối ưu thì mean-squared error ứng với nó càng nhỏ và ngược lại. Bằng việc sử dụng giải tích, ta có thể chứng minh rằng $J$ là một hàm lồi liên tục trên $R^n$, do đó, chúng ta có thể áp dụng thuật toán Gradient Descent để tìm ra nghiệm của bài toán (các bạn có thể xem bài viết về Gradient Descent của mình tại đây). Nếu các bạn có kiến thức về giải tích đa chiều, có thể tìm được vector Jacobi của $J$ là
\[\overrightarrow{\nabla} J(\overrightarrow{w})=X^T(X\overrightarrow{w} - \overrightarrow{y})\]với
\[X = \left[ \begin{array}{l} 1 & x_{1, 1} & x_{1, 2} & \cdots & x_{1, n}\\ 1 & x_{2, 1} & x_{2, 2} & \cdots & x_{2, n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{m, 1} & x_{m, 2} & \cdots & x_{m, n} \end{array} \right], \overrightarrow{w} = \left[ \begin{array}{l} w_1\\ w_2\\ \vdots\\ w_n \end{array} \right], \text { và } \overrightarrow{y} = \left[ \begin{array}{l} y_1\\ y_2\\ \vdots\\ y_m \end{array} \right]\tag{1}\label{eq:01}\]Như vậy, thuật toán Gradient Descent cho bài toán hồi qui tuyến tính có thể được thiết lập như sau:
- Khởi tạo giá trị ban đầu $w_0$ và thiết lập ma trận $X$ và vector $y$ như trên.
- Thực hiện một lượng lớn vòng lặp cho đến khi $\overrightarrow{w}_n$ hội tụ. Tại vòng lặp thứ i, thực hiện các bước sau:
- Tính vector Jacobi ứng với $\overrightarrow{w}_{i-1}$: $\overrightarrow{\nabla} J(\overrightarrow{w}_{i-1}) = X^T\left(X\overrightarrow{w}_{i-1} - \overrightarrow{y}\right).$
- Tính trọng số mới tối ưu hơn trọng số cũ $\overrightarrow{w}_i = \overrightarrow{w}_{i-1} - \alpha * \overrightarrow{\nabla} J(\overrightarrow{w}_{i-1})$ với $\alpha$ là tốc độ học (learning rate).
Như vậy sau một lượng lớn vòng lặp thì vector $\overrightarrow{w}_n$ sẽ hội tụ đến nghiệm tối ưu.
Để lấy ví dụ ứng dụng thực tế của thuật toán, giả sử bạn cần ước lượng giá ngôi nhà của bạn với diện tích khoảng 100 mét vuông trên thị trường để bán căn nhà của bạn. Bước đầu tiên của bạn luôn luôn phải là khảo sát thị trường thu thập giá của nhiều ngôi nhà với diện tích khác nhau. Giả sử bước này đã thực hiện xong và bạn có tập dữ liệu như mô tả bên dưới.
| Diện tích (m2) | Giá (triệu VNĐ) |
|---|---|
| 1 | 2.72 |
| 6 | 4.47 |
| 12 | 7.6 |
| 17 | 10.76 |
| 23 | 12.92 |
| 28 | 19.02 |
| 34 | 18.17 |
| 40 | 22.5 |
| 45 | 21.06 |
| 50 | 23.84 |
Khi lấy trục x là diện tích nhà và trục y là giá nhà thì bạn sẽ có hình dưới đây.
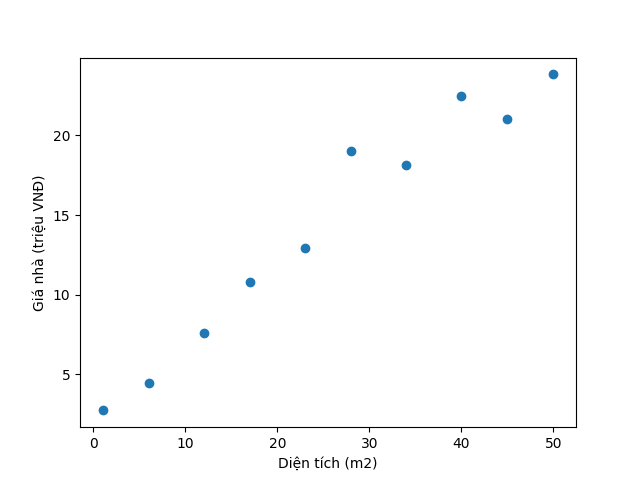
Rõ ràng biểu đồ trên cho ta thấy mỗi điểm dữ liệu gần như nằm trên một đường thẳng. Và chúng ta cần phải tìm đường thẳng đó để có thể ước lượng giá nhà của mình. Như vậy đầu tiên bạn phải thiết lập ma trận $X$ và vector $\overrightarrow{y}$.
\[X = \left[ \begin{array}{l} 1 & 1 \\ 1 & 6 \\ 1 & 12 \\ 1 & 17 \\ 1 & 23 \\ 1 & 28 \\ 1 & 34 \\ 1 & 40 \\ 1 & 45 \\ 1 & 50 \\ \end{array} \right]\text{ và } \overrightarrow{y}=\left[ \begin{array}{l} 2.72\\ 4.47\\ 7.6\\ 10.76\\ 12.92\\ 19.02\\ 18.17\\ 22.5\\ 21.06\\ 23.84 \end{array} \right]\]Sau khi đã thiết lập $X$ và $\overrightarrow{y}$, bạn chỉ cần khởi tạo $w_0$ có chiều $2\times 1$ và tạo một vòng lặp (tầm 500 vòng) thực hiện các bước như đã đề cập ở trên là sẽ tìm được bộ tham số tối ưu để ước lượng giá nhà của bạn. Dưới đây là một ví dụ của việc sử dụng Python để chạy bài toán trên với 500 vòng lặp.
# mình sử dụng thư viện numpy để hỗ trợ việc tính ma trận
# các bạn có thể tham khảo nó tại: https://numpy.org
import numpy as np
# Đầu tiên, mình thiết lập ma trận X và vector y
X = np.array([[1, 1],
[1, 6],
[1, 12],
[1, 17],
[1, 23],
[1, 28],
[1, 34],
[1, 40],
[1, 45],
[1, 50]])
y = np.array([[2.72],
[4.47],
[7.6],
[10.76],
[12.92],
[19.02],
[18.17],
[22.5],
[21.06],
[23.84]])
# Sau đó mình khởi tạo vector w.
# Ở đây mình cứ chọn đại vector 0 có chiều 2x1
# Các bạn có thể khởi tạo random
w = np.array([[0],
[0]])
# Cuối cùng mình chạy 1 vòng lặp 500 vòng
# và thu được nghiệm của bài toán
# Các bạn có thể sử dụng các điều kiện dừng khác như
# nếu bộ tham số ở iteration sau không lớn hơn nhiều so với bộ tham số trước thì dừng
learning_rate = 0.0001
for _ in range(500):
jacob_vector = np.dot(X.T, X.dot(w_0) - y)
w = w - learning_rate * jacob_vector
print(w)
# Nếu bạn muốn predict giá nhà thì chạy đoạn code này là có thể tìm được giá nhà của bạn.
# Thế là bạn có thể bán nhà thành công :D
X_new = np.array([[1, 100]])
print(X_new.dot(w))
Dưới đây là hình minh hoạ cho quá trình huấn luyện của thuật toán hồi qui tuyến tính.
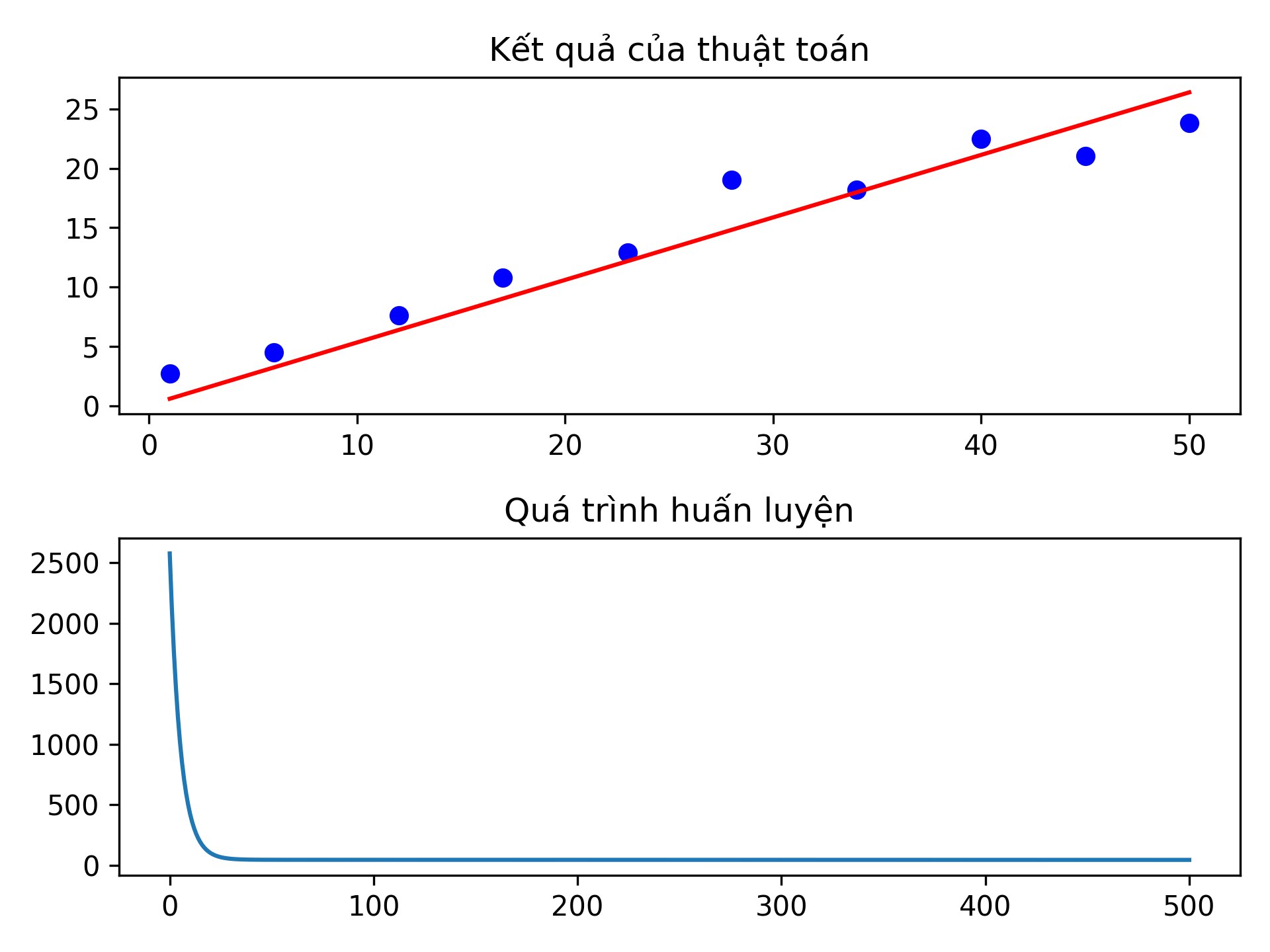
Như các bạn thấy, nếu thuật toán của các bạn được thực thi thành công thì khi bạn vẽ đường thẳng dự đoán, khoảng cách giữa mỗi điểm đến đường dự đoán rất nhỏ (hình trên). Hơn nữa, để có thể phát hiện ra sai sót trong quá trình thực thi, các bạn có thể vẽ biểu đồ đường với trục x thể hiện vòng lặp và trục y thể hiện giá trị của hàm mất mát. Nếu tốc độ học được chọn phù hợp và bạn không tính sai đạo hàm, biểu đồ sẽ có dạng giảm dần vào những vòng lặp ban đầu và phẳng dần với những vòng lặp lớn hơn (hình dưới).
Nếu bạn đọc được đến đây rồi thì chúc mừng! Bạn đã có đủ kiến thức để bước tiếp vào các thuật toán cao hơn rồi. Đó là những gì bạn được nghe khi bạn học được đến đây từ những người dạy ở ngoài. Tuy nhiên, với mình, điều này là chưa đủ để tận dụng hết sức mạnh của thuật toán hồi qui tuyến tính. Làm sao để có thể hiểu hết và tận dụng hết được thuật toán này thì mời các bạn đến phần tiếp theo.
Góc nhìn xác suất của thuật toán hồi qui tuyến tính
Có thể các bạn không biết (hoặc đã biết) nhưng hầu hết các thuật toán học giám sát có sử dụng tham số đều được xây dựng dựa trên phương pháp maximum likelihood estimation (MLE, tên tiếng Việt là hợp lí cực đại nhưng mà tên này nó sai quá nên thôi mình giữ phiên bản tiếng Anh của nó). Phương pháp này cụ thể đưa ra một ước lượng tốt nhất về một tham số chưa biết bằng việc cực đại hoá phân phối của dữ liệu thu được nếu biết dữ liệu được lấy mẫu từ một phân bố xác suất bị chi phối bởi tham số chưa biết đó (likelihood). Ví dụ, bạn muốn tính chiều cao trung bình của người Việt Nam thì bạn phải lấy trung bình của 96 triệu dân. Thế nhưng bạn không thể đủ sức làm được việc đó (ngay cả việc khảo sát dân số cũng không thể thực hiện trên toàn bộ dân số Việt Nam mà chỉ thực hiện trên một lượng lớn dân số). Như vậy, việc bạn làm là đi hỏi khoảng 50-100 người Việt Nam về chiều cao và tính trung bình rồi cho ra kết quả. Việc tính trung bình đó là kết quả của việc sử dụng phương pháp MLE trên phân phối của dữ liệu bạn thu được biết dữ liệu được lấy mẫu từ một phân phối chuẩn với giá trị trung bình là tham số cần tìm và phương sai được xem là đã biết dựa trên các nghiên cứu thực nghiệm.
Trong khuôn khổ bài viết này, mình sẽ sử dụng phương pháp này để cho các bạn thấy tại sao phải sử dụng hàm mean-squared error như trên để tìm ra bộ tham số tối ưu và những suy diễn liên quan đến nó (bạn cũng có thể áp dụng phương pháp này để tìm chiều cao trung bình của người Việt Nam). Để sử dụng phương pháp này trước hết chúng ta cần phát biểu lại bài toán hồi qui tuyến tính một chút để các bạn có thể thấy khía cạnh xác suất của nó:
\[Y=\beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_nX_n+\epsilon\]Giả sử ta có $n$ biến ngẫu nhiên tương ứng với $n$ thuộc tính trong dữ liệu $X_1$, $X_2$, $\ldots$, $X_n$ và một biến Y có quan hệ tuyến tính với các thuộc tính hay nói cách khác (đây là giả sử của bài toán hồi qui tuyến tính):
Sau đó, chúng ta lấy mẫu ngẫu nhiên dựa trên phân phối của $X_1, X_2, X_3, \ldots, X_n, Y$ và thu được một tập dữ liệu $\mathcal{D} = \{(x_{i,1}, x_{i,2},\ldots, x_{i,n}, y_i)| i=\overline{1,m}\}$ (đây chính là bước thu thập dữ liệu).
Như vậy, chúng ta cần phải tìm bộ tham số $(\widehat{\beta}_1, \widehat{\beta}_2, \ldots, \widehat{\beta}_n)$ các bộ tham số này “gần” với bộ tham số $(\beta_0, \beta_1,\ldots,\beta_n)$ nhất dựa trên tập dữ liệu $\mathcal{D}$.
Để có thể sử dụng phương pháp MLE, chúng ta cần phải tìm phân phối tham số này biết dữ liệu mà chúng ta thu được $\mathcal{D}$. Nói một cách toán học tức là bạn phải tính được hàm phân phối xác suất $p(d_1, d_2,\ldots, d_n | \beta_1, \beta_2, \ldots, \beta_n)$ với $d_i = (x_{i,1}, x_{i,2},\ldots, x_{i,n}, y_i)$. Ở đây, nếu chúng ta giả sử $\epsilon\sim\mathcal{N}(0, \sigma^2)$ thì rõ ràng
\[Y\sim p(y)=\mathcal{N}(\beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_nX_n, \sigma^2).\]Như vậy nếu $y_1$, $y_2$, $\ldots$, $y_m$ được lấy mẫu ngẫu nhiên độc lập từ $p(y)$ thì rõ ràng
\[\begin{align*} p(d_1, d_2, \ldots, d_n|\beta_0, \beta_1, \ldots, \beta_n) &= \prod_{i=1}^m p(d_i|\beta_0, \beta_1, \ldots, \beta_n)\\ &= \prod_{i=1}^m \dfrac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\dfrac{(y_i - \beta_0 - \beta_1x_{i,1} - \beta_2x_{i,2} - \ldots - \beta_nx_{i,n})^2}{2\sigma^2}\right\}\\ &\propto\exp\left\{-\dfrac{\sum_{i=1}^n(y_i - \beta_0 - \beta_1x_{i,1} - \beta_2x_{i,2} - \ldots - \beta_nx_{i,n})^2}{2\sigma^2}\right\} \end{align*}\]Hàm $p(d_1, d_2, \ldots, d_n|\beta_0, \beta_1, \ldots, \beta_n)$ còn có một tên gọi khác nữa là hàm likelihood. Như vậy, như tên gọi của phương pháp MLE, chúng ta cần phải tìm bộ tham số $(\widehat{\beta}_1, \widehat{\beta}_2, \ldots, \widehat{\beta}_n)$ để hàm likelihood đạt giá trị lớn nhất. Chúng ta có thể tính đạo hàm trực tiếp của hàm likelihood để tìm ra kết quả hoặc lấy log hai vế rồi tìm giá trị cực đại của hàm log (lưu ý lấy log của một hàm số không làm thay đổi tính biến thiên, lồi lõm của hàm số đó).
\[\begin{align*} \log p(d_1, d_2, \ldots, d_n|\beta_0, \beta_1, \ldots, \beta_n) = -\dfrac{1}{2\sigma^2}\sum_{i=1}^n(y_i - \beta_0 - \beta_1x_{i,1} - \beta_2x_{i,2} - \ldots - \beta_nx_{i,n})^2 \end{align*}\]Đây rõ ràng tương ứng với việc cực tiểu hoá mean-squared error sử dụng thuật toán Gradient Descent như đã đề cập ở phía trước và cũng là nguồn gốc của việc sử dụng mean-squared error để tìm ra bộ tham số tốt nhất. Hơn nữa, chúng ta còn có thể biết nghiệm tối ưu chuẩn tắc của bài toán trên là $\widehat{\beta} = (X^TX)^{-1}X^Ty$. Tuy nhiên việc sử dụng nghiệm chuẩn tắc để giải bài toán hồi qui tuyến tính không được khuyến khích để sử dụng trong ứng dụng thực tế vì độ phức tạp của việc tính ma trận nghịch đảo không phù hợp để triển khai.
Chính vì bản chất của hàm mean-squared error là việc sử dụng phương pháp MLE. Cho nên chúng ta cần phải biết được:
-
Ước lượng về tham số $\beta$ này có unbiased không (nói một cách khác là kì vọng của ước lượng $\widehat{\beta}$ phải đúng bằng với tham số $\beta$ chưa biết)
-
Làm sao để tính được khoảng tin cậy (confidence interval) của ước lượng này để có thể đánh giá liệu mô hình này có thể ứng dụng cho thực tế hay không?
Để trả lời câu hỏi 1, tất nhiên chúng ta phải tính kì vọng của $\widehat{\beta}$.
\[\mathbb{E}[\widehat{\beta}] = \mathbb{E}[(X^TX)^{-1}X^Ty] = (X^TX)^{-1}X^T\mathbb{E}[y] = (X^TX)^{-1}X^TX\beta = \beta\tag{2}\label{eq:02}\]Như vậy có thể thấy được $\widehat{\beta}$ là một ước lượng unbiased. Câu hỏi thứ hai được trả lời từ hai quan sát sau (mình sẽ chứng minh nó trong phần Phụ lục).
- $\widehat{\beta}\sim\mathcal{N}\left(\beta, \sigma^2(X^TX)^{-1}\right)$
- Đặt $S = \lVert y - X\widehat{\beta}\rVert_2^2$. Như vậy thì $\dfrac{S}{\sigma^2}\sim\chi_{m-n-1}^2$.
Như vậy, rõ ràng nếu đặt A = $(X^TX)^{-1}$ thì $\widehat{\beta}_i\sim\mathcal{N}(\beta_i, \sigma^2\times A_{ii})$, do đó
\[\dfrac{\widehat{\beta_i} - \beta_i}{\sqrt{\dfrac{A_{ii}\times S}{m-n-1}}}\sim T_{m-n-1}\]Như vậy, với mức độ tin cậy $1-\alpha$, khoảng tin cậy của $\widehat{\beta_i}$ sẽ là
\[\left[\widehat{\beta}_i-t_{\alpha/2, m-n-1}\sqrt{\dfrac{A_{ii}\times S}{m-n-1}}, \widehat{\beta}_i+t_{\alpha/2, m-n-1}\sqrt{\dfrac{A_{ii}\times S}{m-n-1}}\right]\]Ngoài ra, nếu bạn áp dụng khoảng tin cậy lên $\widehat{y} = X\widehat{\beta}$, bạn cũng có thể tìm ra được khoảng tin cậy của nó và thu được hình bên dưới về kết quả của thuật toán với ví dụ bên trên với khoảng tin cậy $95\%$.
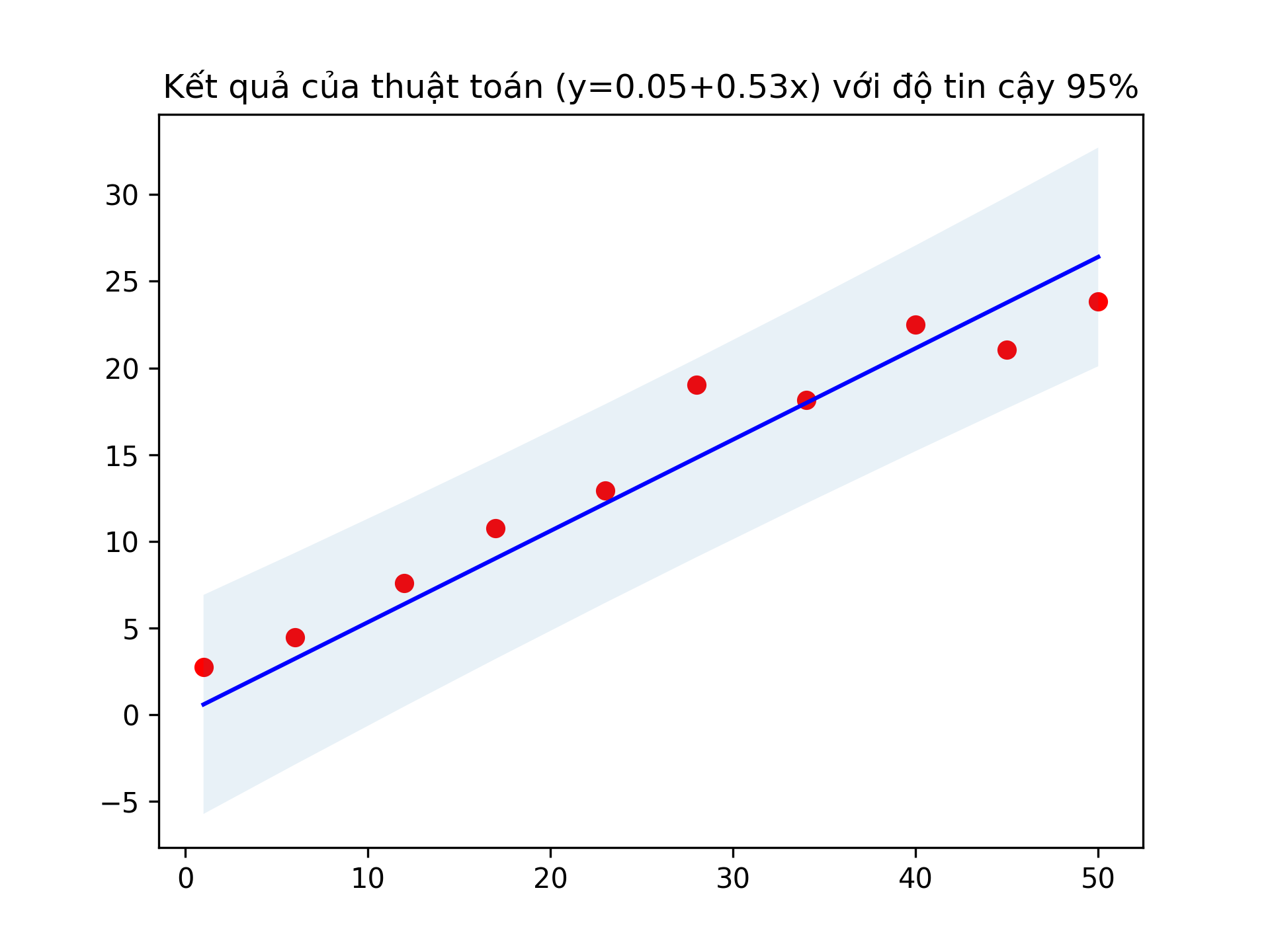
Đây chính là góc nhìn đầy đủ và toàn diện nhất về bài toán hồi qui tuyến tính. Việc sử dụng phân phối mẫu của ước lượng tham số sẽ giúp bạn quyết định xem mô hình tuyến tính bạn xây dựng được có đáng tin cậy hay không. Nếu mô hình ước lượng được các tham số $\widehat{\beta}_i$ nhưng lại có khoảng tin cậy rất lớn thì có khả năng mô hình của bạn đã không mô hình hoá tốt mối quan hệ giữa nhãn và thuộc tính, ngược lại, nếu khoảng tin cậy nhỏ thì mô hình xây dựng được là đáng tin cậy và có thể sử dụng vào các ứng dụng thực tế.
Hiểu biết được khía cạnh xác suất của bài toán hồi qui tuyến tính còn cho phép bạn lọc bỏ những thuộc tính không cần thiết. Điều này được thực hiện bằng việc sử dụng kiểm định giả thuyết xác suất (hypothesis testing) với giả thuyết rỗng (null hypothesis) $H_0: \beta_i=0$ và giả thuyết thay thế (alternative hypothesis) $H_a: \beta_i\neq 0$. Như vậy, với hệ số sig (significant level) $\alpha$,
-
Nếu $|\widehat{\beta}_i| > t_{\alpha / 2, m-n-1}\sqrt{\dfrac{A_{ii}\times S}{m - n - 1}}$ thì ta bác bỏ giả thuyết rỗng và chấp nhận giả thuyết thay thế. Tức là có một mối liên hệ giữa nhãn và thuộc tính $i$.
-
Ngược lại, nếu $|\widehat{\beta}_i| \leq t_{\alpha / 2, m-n-1}\sqrt{\dfrac{A_{ii}\times S}{m - n - 1}}$ thì ta chấp nhận giả thuyết rỗng. Tức là không hề có mối liên hệ nào giữa nhãn và thuộc tính i. Và ta có thể bỏ thuộc tính đó đi và xây dựng lại mô hình.
Kết luận
Việc sử dụng xác suất thống kê lên thuật toán hồi qui tuyến tính giúp cho thuật toán này trở nên cực kì hữu dụng không chỉ trong việc tìm ra mối tương quan giữa các biến với nhau mà còn giúp loại bỏ những biến không quan trọng gây nhiễu cho quá trình huấn luyện. Thuật toán hồi qui tuyến tính đã được sử dụng để làm nền cho rất nhiều thuật toán cao cấp sau này, bao gồm cả các mạng nơ-ron phức tạp. Tuy nhiên, thuật toán hồi qui tuyến tính vẫn còn nhiều hạn chế. Hạn chế đầu tiên là thuật toán hồi qui tuyến tính, đúng như tên gọi của nó, chỉ có thể biểu diễn được các mối quan hệ tuyến tính mà thiếu khả năng biểu diễn các mối quan hệ phi tuyến. Việc này tuy có thể cải thiện bằng việc phức tạp hoá thuộc tính bằng cách thêm các thuộc tính bậc cao nhưng lại dẫn đến tiềm tàng bị overfit trong quá trình huấn luyện. Hạn chế thứ hai là thuật toán hồi qui tuyến tính cực kì nhạy cảm với các điểm dữ liệu ngoại vi (outlier). Lí do là các hạng tử ứng với các điểm dữ liệu ngoại vi trong mean-squared error thường mang các giá trị rất lớn (do bình phương của một số cực lớn sẽ tạo ra một số lớn hơn), do đó việc xử lí dữ liệu là tối quan trọng trước khi áp dụng thuật toán này.
Phụ lục
Ở phần này mình sẽ chứng minh 2 quan sát được đề cập ở phần 3 của bài viết. Quan sát thứ nhất rất dễ thấy nếu bạn sử dụng các biến đổi đại số tuyến tính với lưu ý nếu ma trận hiệp phương sai của vector biến ngẫu nhiên X là $\Sigma$ thì ma trận hiệp phương sai của $AX$, với $A$ là một ma trận, sẽ là $A\Sigma A^T$). Để chứng minh được quan sát thứ hai mình cần chứng minh hai bổ đề sau:
Bổ đề 1
Nếu $A$ là một ma trận luỹ đẳng đối xứng với chiều $n\times n$ thì tồn tại một ma trận $U$ có chiều $n\times r$ với $r$ là hạng của ma trận $A$ sao cho $A = UU^T$.
Chứng minh: Vì $A$ là một ma trận luỹ đẳng nên các trị riêng của ma trận $A$ chỉ có thể là 0 hoặc 1. Mặt khác vì $A$ cũng là ma trận đối xứng nên theo định lí phổ, $A = UDU^T$ với $D$ là một ma trận chéo chứa các trị riêng của ma trận $A$ và ma trận $U$ là ma trận trực giao với các cột là các vector riêng tương ứng với trị riêng. Mặt khác, do $r$ là hạng của ma trận $A$ nên có tất cả $r$ trị riêng bằng 1. Vậy nên nếu bỏ tất cả các trị riêng bằng 0 và các vector riêng tương ứng, ta sẽ thu được ma trận $D$ mới đúng bằng với ma trận đơn vị có chiều là $r\times r$ và ma trận $U$ mới có chiều là $n\times r$ mà vẫn đảm bảo $A = UDU^T = UIU^T = UU^T$. Từ đó, ta có điều phải chứng minh. $\blacksquare$
Bổ đề 2
Nếu ta có $Z$ là một vector thuộc $\mathbb{R}^n$ gồm các biến ngẫu nhiên độc lập lấy từ phân phối chuẩn chuẩn hoá (hay nói cách khác, $Z\sim\mathcal{N}(0, I)$ với $I$ là ma trận đơn vị có chiều $n\times n$) và $A$ (cũng số chiều $n\times n$) là một ma trận luỹ đẳng đối xứng. Khi đó, $Z^TAZ$ sẽ là biến ngẫu nhiên có phân phối $\chi^2$ với bậc tự do là hạng của ma trận $A$.
Chứng minh: Sử dụng bổ đề 1, ta thấy tồn tại một ma trận trực giao $U$ có chiều $n\times r$ thoả mãn $A = UU^T$. Do đó, $Z^TAZ = Z^TUU^TZ$. Mặt khác, nếu đặt $Z’=U^TZ$ thì rõ ràng $Z’\sim\mathcal{N}(0, I)$ thuộc $\mathbb{R}^r$ với $r$ là bậc của ma trận $A$. Do đó, $Z^TAZ = Z’^TZ’$ chính là biến ngẫu nhiên $\chi^2$ với bậc tự do là hạng của ma trận $A$. $\blacksquare$
Quay trở lại bài toán của chúng ta, nếu viết lại $S$ dưới dạng ma trận thì ta sẽ có $S = y^T(I-H)y$ với $I$ là ma trận đơn vị có số chiều là $n$, và $H = X(X^TX)^{-1}X^T$ (X, y được thiết kế tại ($\ref{eq:01}$)). Như vậy $S\sim\sigma^2\chi^2_r$ với $r$ là hạng của ma trận $I - H$. Mặt khác, dễ dàng chứng minh $I - H$ là ma trận luỹ đẳng đối xứng nên ta có
\[\begin{align*} rank(I - H) &= trace(I - H) = trace(I) - trace(H) = n - trace(X(X^TX)^{-1}X^T) \\ &= m - trace((X^TX)^{-1}X^TX) = m - n - 1. \end{align*}\]Do đó, ta có $\frac{S}{\sigma^2}\sim\chi^2_{m-n-1}$. Từ đó, ta chứng minh được quan sát thứ hai.
