Giới thiệu
Chuyện là bây giờ mình sắp kết thúc năm ba rồi và đang trong quá trình chuẩn bị thực tập. Nhưng mà portfolio của mình yếu quá nên giờ mình sẽ quay trở lại viết blog tiếp. Rất may mắn là mình kiếm được một chủ đề không mấy là mới nhưng lại khá là quan trọng trong quá trình học của mình. Mặc dù trường mình có dạy phương pháp này nhưng giáo viên dạy rất là khô khan và lan man (đây cũng là động lực chính để mình viết blog này). Mình mong bài viết này tuy ngắn nhưng sẽ bao quát hết được ý tưởng đằng sau của thuật toán và các khảo sát lí thuyết của thuật toán về tốc độ hội tụ.
Thuật toán Gradient Descent lần đầu tiên được tìm ra bởi nhà toán học nổi tiếng Cauchy (cũng là nhân vật ám ảnh với các bạn học sinh cấp 2 với những bài toán bất đẳng thức khó). Sau đó phương pháp này được nghiên cứu bởi Haskell Cury (cha đẻ của ngôn ngữ lập trình Haskell, đi đầu về phong cách lập trình hướng hàm (functional programming)) và từ đó, Gradient Descent khá nổi tiếng trong giới khoa học dưới cái tên steepest descent.
Bài blog này sẽ được chia làm ba phần với mức độ khó tăng dần: phần đầu mình sẽ giới thiệu về ý tưởng đằng sau thuật toán Gradient Descent, phần hai mình sẽ chứng minh tại sao thuật toán Gradient Descent có thể hoạt động được, và phần cuối sẽ khảo sát về tốc độ hội tụ của thuật toán.
Ý tưởng của thuật toán
Hồi xưa khi còn học cấp 3, mình được các thầy cô giảng về cách tìm cực trị bằng việc sử dụng đạo hàm. Ví dụ như tìm giá trị nhỏ nhất của hàm số $y=x^2$ trên tập số thực chẳng hạn. Bước đầu tiên cần làm đó chính là tính đạo hàm của nó, đó là $y’=2x$. Rồi sau đó giải phương trình $y’=0$ để tìm ra các giá trị cực trị x (hàm số này có 1 điểm cực trị là x=0). Tiếp đó, bạn phải khảo sát hàm số trên các khoảng được chia bởi các điểm cực trị (trong trưởng hợp này là $(-\infty, 0)$ và $(0, \infty)$). Cuối cùng, sau khi khảo sát xong bạn kết luận $y$ đạt GTNN khi $x=0$. Cách làm này khá hợp lí nhưng có nhiều bước quá dư thừa: không nhất thiết phải khảo sát hàm số thì mới tìm ra được GTNN (tại sao phải khảo sát toàn bộ hàm số chỉ để giải phương trình $y’=0$ cho ra kết quả?). Nếu bạn là một học sinh Chuyên toán (hoặc trường bạn không giảm tải chương này) thì bạn sẽ được biết đến một cách giải ngắn hơn hiệu quả hơn dựa trên một định lí đề cập Sách giáo khoa:
Định lí 1: Cho một hàm số $f(x)$ liên tục trên $\mathbb{R}$.
Khi đó, điểm $x_0$ được gọi là:
điểm cực tiểu nếu $f’(x_0) = 0$ và $f”(x_0) > 0$.
điểm cực đại nếu $f’(x_0)=0$ và $f”(x_0) < 0$.
Định lí này giúp cho việc tìm cực tiểu hoặc cực đại của hàm số trở nên dễ dàng hơn không chỉ về mặt toán học mà còn về mặt lập trình (trên thực tế, các thuật toán tối ưu hoá trong lĩnh vực Khoa học Máy tính đều cố gắng chuyển hoá các bài toán cực trị thành các bài toán giải phương trình và hệ phương trình rồi sử dụng các phương pháp lặp để tìm ra nghiệm của bài toán). Định lí 1 là tiền đề cho phương pháp Newton-Raphson trong việc tìm giá trị cực tiểu (hoặc cực đại) của một hàm số lồi (hoặc lõm). Ý tưởng rất đơn giản: giả sử $f$ đã được chứng minh là một hàm lồi (hoặc lõm), điểm tối ưu của $f$ chính là nghiệm của phương trình $f’(x) = 0$ và cũng là điểm hội tụ của dãy số $(x_n)$ xác định bởi:
\[\left\{\begin{array}{l} x_0\\ x_{n + 1} = x_n - \dfrac{f'(x_n)}{f''(x_n)}\forall n\geq 0 \end{array}\right.\]Phương pháp Newton-Raphson hiệu quả về mặt lí thuyết và có nhiều ứng dụng trong thực tế (như chức năng giải nghiệm trên các máy tính cầm tay có mặt trên thị trường). Tuy nhiên, khi nói đến khía cạnh ứng dụng, phương pháp này gặp phải 2 trở ngại lớn:
-
Phương pháp này đòi hỏi việc chọn $x_0$ rất gần so với nghiệm thực tế của bài toán, nếu không dãy số thiết lập rất dễ bị phân kì.
-
Trong các bài toán hàm số đa biến, việc này đòi hỏi phải tính nghịch đảo của ma trận Hessian. Tính đến hiện tại, các thuật toán tính nghịch đảo của ma trận đòi hỏi độ phức tạp thời gian và không gian rất lớn. Do đó, tuy tốc độ hội tụ của phương pháp Newton-Raphson nhanh, bộ nhớ và thời gian thực thi của phương pháp có thể sẽ hết trước khi bài toán hội tụ.
Có thuật toán nào chỉ cần tìm ra đạo hàm bậc 1 có thể suy ra được nghiệm tối ưu của hàm $f$ (nếu $f$ là hàm lồi hoặc lõm)? Đó là ý tưởng chính của thuật toán Gradient Descent. Phát biểu của thuật toán rất đơn giản như sau:
\[\left\{\begin{array}{l} x_0\\ x_{n + 1} = x_n - \alpha_n * f'(x)\forall n\geq 0 \end{array}\right.\]Cho hàm số lồi $f$ và dãy số $(x_n)$ được định nghĩa bởi:
Khi đó tồn tại dãy số không âm $(\alpha_n)$ để dãy số $(x_n)$ hội tụ về điểm cực tiểu.
Về chứng minh toán học, mình sẽ đề cập ở phần sau. Ở phần này, mình muốn cho các bạn thấy ý tưởng đằng sau thuật toán này. Ý tưởng xuất phát từ một quan sát rất tầm thường với các bạn học sinh cấp 3: nếu f giảm trên đoạn $[a, b]$ thì $f’(x)\leq 0$ và ngược lại nếu $f$ tăng trên đoạn $[a, b]$ thì $f’(x)\geq 0$. Vậy nếu chọn đại một điểm $(x_0, f(x_0))$ và $x_0$ nằm bên trái điểm cực tiểu thì $f’(x_0) < 0$ (giả sử f là hàm lồi) nên $x_1$ sẽ di chuyển về bên phải, tức là hướng về điểm cực tiểu (Minh hoạ bên dưới).
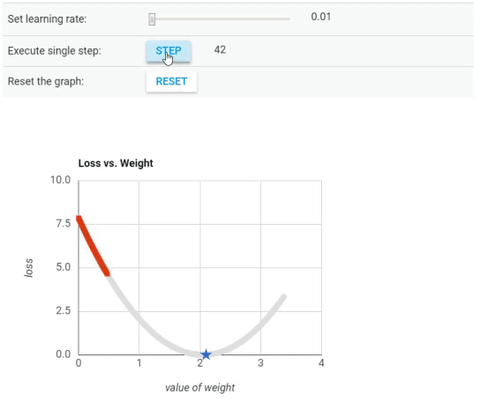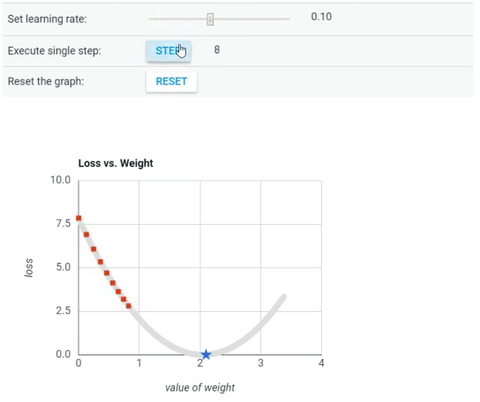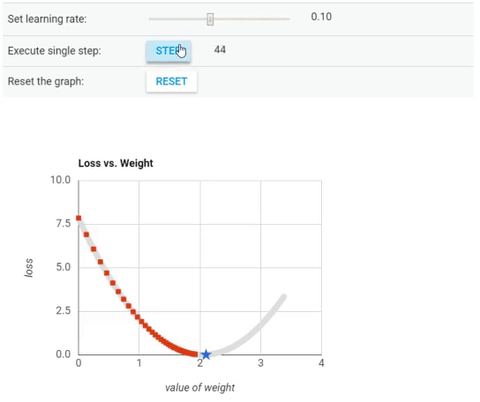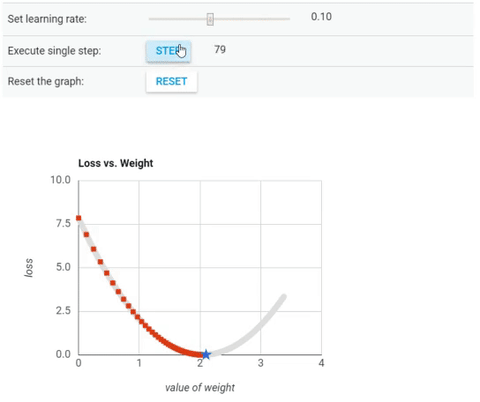
Ở hình này, người minh hoạ đang chỉnh alpha_n=0.1 với mọi n (dòng đầu tiên)
và chạy từng bước của thuật toán gradient descent. Như các bạn thấy, do
x0 nằm bên tay trái điểm cực tiểu nên x1 sẽ được cộng một lượng dương từ x0
và di chuyển về bên phải, tiến về điểm cực tiểu.
Lí luận tương tự, nếu $x_0$ nằm bên tay phải của điểm cực tiểu thì $f’(x_0) > 0$ và $x_1$ sẽ đi về bên trái, cũng hướng về điểm cực tiểu.
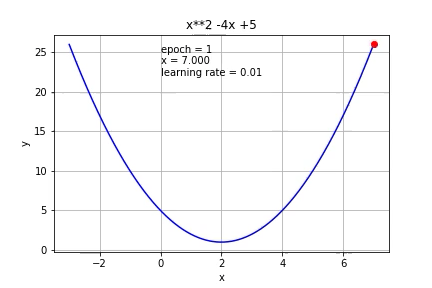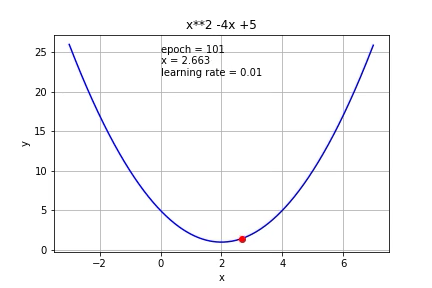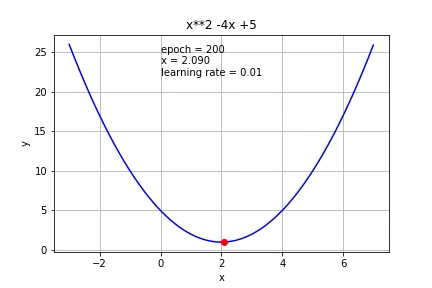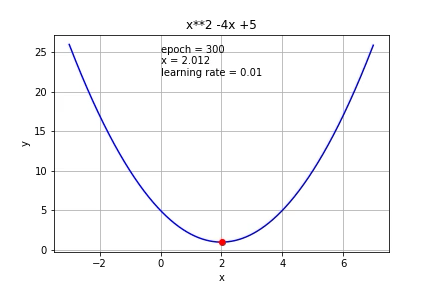
Ở hình này, người minh hoạ đang chỉnh alpha_n=0.01 với mọi n (dòng đầu tiên)
và chạy từng bước của thuật toán gradient descent. Như các bạn thấy, do
x0 nằm bên tay phải điểm cực tiểu nên x1 sẽ bị trừ đi một lượng từ x0
và di chuyển về bên trái, tiến về điểm cực tiểu.
Nếu bạn tinh ý, bạn sẽ thắc mắc liệu $x_n$ có thể di chuyển quá điểm cực tiểu không? Câu trả lời là có nếu bạn chọn dãy $(\alpha_n)$ không phú hợp ($\alpha_n$ quá lớn với mọi n). Tưởng tượng dãy $(\alpha_n)$ không phù hợp giống như bạn chơi cầu trượt khi chạm đến đáy có bôi nhớt bạn sẽ phải trượt ra thêm một đoạn nữa (và té dập mặt) thì trường hợp này cũng giống như vậy. Chính vì điều này mà $(\alpha_n)$ có một tên gọi khác là tốc độ học (tên tiếng Anh là learning rate). Hình phía dưới minh hoạ cho việc gradient descent thất bại khi chọn tốc độ học quá lớn.
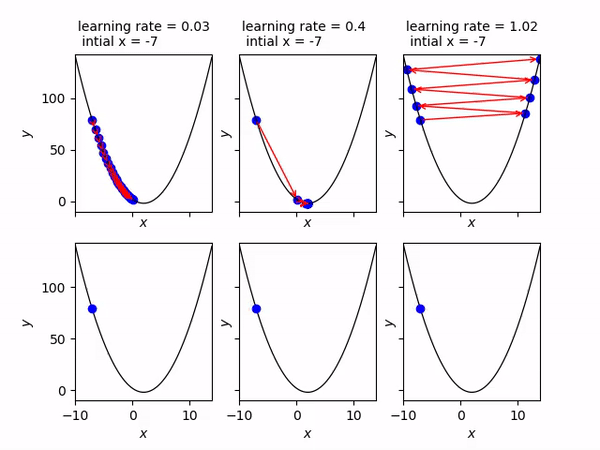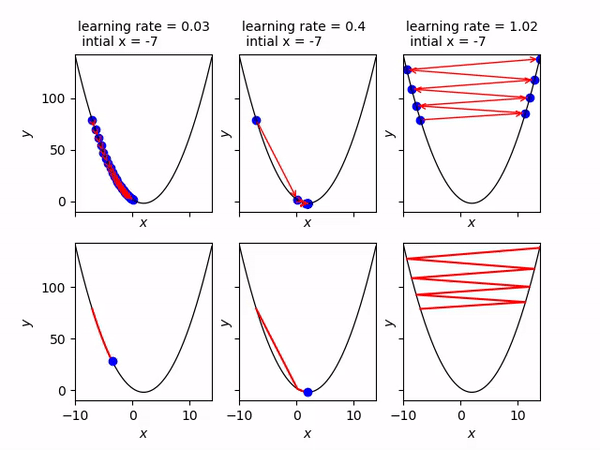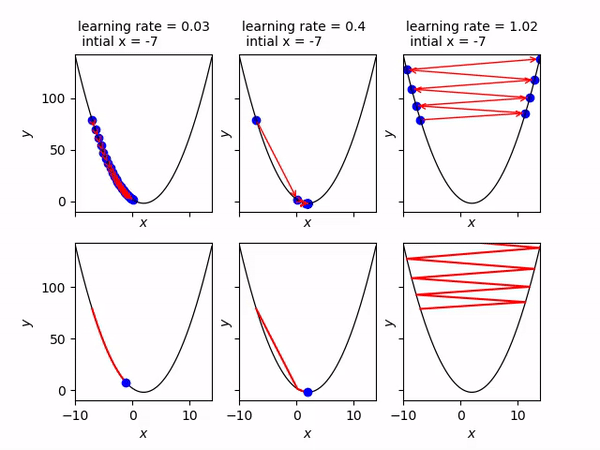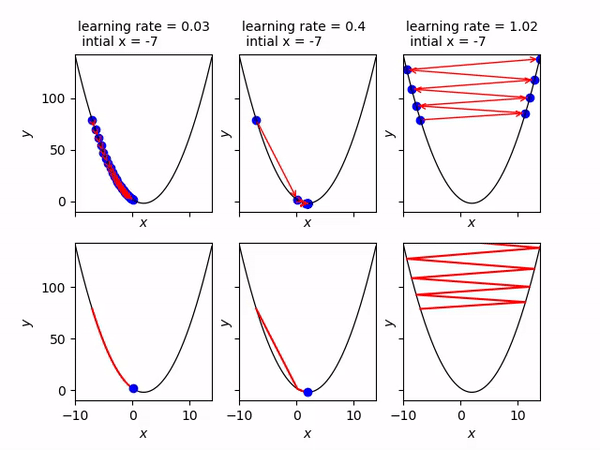
Ở hình này, từ trái qua phải là các trường hợp chọn tốc độ học alpha_n bằng 0.03, 0.4, 1.02.
Nếu chọn 0.03 thì x_n sẽ đi chậm về phía điểm cực tiểu.
Nếu chọn 0.4 thì x_n sẽ nhanh chóng hội tụ về điểm cực tiểu.
Nếu chọn 1.02 thì x_n sẽ lạng lách và đi càng ngày càng xa điểm cực tiểu.
Vậy làm sao để chọn tốc độ học phù hợp? Đây là một câu hỏi mở cho thuật toán Gradient Descent. Thông thường, tốc độ học sẽ nằm vào trong khoảng $(0, 1)$ và thường được cố định bằng 1 hằng số qua các vòng lặp. Tuy nhiên, cách này không hiệu quả cho các ứng dụng lớn có dữ liệu nhiều chiều. Chính vì thế, đã có rất nhiều thuật toán giải quyết vấn đề chọn $(\alpha_n)$ bằng việc xây dựng dãy $(\alpha_n)$ thích nghi với từng vòng lặp. Nhưng đó sẽ là chủ đề cho các bài viết sau. Trước khi bước vào phần khảo sát về tính hội tụ của thuật toán, mình xin để phiên bản Gradient Descent cho các hàm số đa biến:
Cho $f:\mathbb{R^n}\to\mathbb{R}$ là một hàm lồi theo mọi biến và dãy vector $(x_n)$ được định nghĩa bởi:
\[\left\{\begin{array}{l} x_0\\ x_{n + 1} = x_n - \alpha_n * \nabla f\forall n\geq 0 \end{array}\right.\]Khi đó tồn tại dãy số không âm $(\alpha_n)$ để dãy vector $(x_n)$ hội tụ về điểm cực tiểu.
Chứng minh sự hội tụ của thuật toán
Trước hết, chúng ta cần phải chứng minh dãy số xây dựng bởi thuật toán trên hội tụ với dãy $(\alpha_n)$ thích hợp. Tất cả các chứng minh kế tiếp đây của mình sẽ thực hiện trên hàm 1 biến nhưng có thể mở rộng ra hàm nhiều biến. Mở rộng thế nào sẽ là phần của các bạn.
Để có thể chứng minh sự hội tụ của thuật toán Gradient Descent, chúng ta cần đến một định lí tổng quát hơn có tên là định lí Bolzano-Weierstrass. Định lí được phát biểu như sau:
Nếu dãy $(x_n)$ đơn điệu tăng và bị chặn trên hoặc đơn điệu giảm và bị chặn dưới thì dãy $(x_n)$ hội tụ.
Chứng minh: Mình sẽ chứng minh với trường hợp dãy đơn điệu tăng. Chứng minh tương tự với dãy đơn điệu giảm.
Do $(x_n)$ là một dãy bị chặn trên nên dãy $(x_n)$ có chặn trên đúng (chặn trên nhỏ nhất). Kí hiệu là $c$. Như vậy, với mọi số $\epsilon > 0$, phải tồn tại một số $n_0$ nào đó thoả $x_{n_0} > c - \epsilon$ (nếu không $c - epsilon$ sẽ là chặn trên đúng của dãy, vô lí). Do $(x_n)$ là một dãy tăng nên ta có thể suy ra được:
với mọi $\epsilon > 0$, tồn tại $n_0$, sao cho với mọi $n > n_0$: $c - \epsilon < x_{n_0} < x_n < c < c + \epsilon\Leftrightarrow |x_n - c| < \epsilon$.
Suy ra được $\lim_{n\to\infty} x_n = c$. Do đó ta có điều phải chứng minh.
Quay về bài toán chính, dễ thấy $x_{n+1} - x_{n} = -\alpha_n f’(x_n)$. Nếu $x_0$ nhỏ hơn điểm cực trị và ta xây dựng dãy $(\alpha_n)$ sao cho $\alpha_n < \frac{x_n - x^*}{f’(x_n)}$ với $x^*$ là điểm cực trị thì dãy $(x_n)$ sẽ trở thành 1 dãy tăng và bị chặn trên bởi $x^*$. Như vậy $(x_n)$ sẽ hội tụ về điểm cực tiểu. Trường hợp $x_0$ lớn hơn điểm cực tiểu với cách tương tự ta cũng có thể thu được dãy $(x_n)$ hội tụ. Vậy suy ra điều phải chứng minh. Như vậy, có thể thấy với dãy $(\alpha_n)$ phù hợp, thuật toán Gradient Descent sẽ đảm bảo sự hội tụ về điểm tối ưu.
Tốc độ hội tụ của Gradient Descent
Một trong những cách đánh giá tốc độ hội tụ của một dãy số là sử dụng kí hiệu $\mathcal{O}$:
Một dãy số $(x_n)$ hội tụ đến $L$ với tốc độ $\mathcal{O}(f(n))$ nếu và chỉ nếu $|x_n - L| = \mathcal{O}(f(n))$.
Chúng ta giả sử hàm $f$ là một hàm đa biến lồi và liên tục L-Lipschitz (tức là $||\nabla f(y) - \nabla f(x)||\leq L ||y-x||$, cần phải giả sử đây là hàm L-Lipschitz để vector gradient không thay đổi đột ngột trong quá trình thực thi). Như vậy, tốc độ hội tụ của thuật toán Gradient Descent là $\mathcal{O}\left(\dfrac{1}{n}\right)$ nếu chọn $\alpha_n = \alpha < \dfrac{1}{L}$ với n là số lần chạy thuật toán Gradient Descent.
Để chứng minh được điều này, chúng ta cần chứng minh bất đẳng thức sau:
\[f(x_n) - f(x^*)\leq\dfrac{\|x_0-x^*\|}{2n\alpha}\]với $x^*$ là điểm cự tiểu, $n$ là số vòng lần thực thi Gradient Descent, và $\alpha$ là tốc độ học.
Do $f$ là một hàm L-Lipschitz nên
\[f(x_n)\leq f(x_{n-1})+\nabla f(x_{n-1})^T(x_n-x_{n-1})+\dfrac{L}{2}\|x_{n}-x_{n-1}\|_2^2\]Mà $x_n - x_{n-1} = -\alpha\nabla f(x_{n-1})$ nên
\[\begin{align} f(x_n)&\leq f(x_{n-1}) + \alpha\|\nabla f(x_{n-1})\|_2^2 + \dfrac{L}{2}\alpha^2\|\nabla f(x_{n-1})\|_2^2\nonumber\\ &=f(x_{n-1}) + \alpha\|\nabla f(x_{n-1})\|_2^2\left(1 - \dfrac{L}{2}\alpha\right)\nonumber\\ &\leq f(x_{n-1}) - \dfrac{\alpha}{2}\|\nabla f(x_{n-1})\|_2^2\label{eq:1} \end{align}\]Do $f$ là một hàm đa biến lồi nên
\[\begin{align} f(x*)\geq f(x_{n-1})+\nabla f(x_{n-1})^T(x^* - x_{n-1})\nonumber\\ \Leftrightarrow f(x_{n-1})\leq f(x^*)+\nabla f(x_{n-1})^T(x_{n-1} - x^*)\label{eq:2} \end{align}\]Thay $(\ref{eq:2})$ vào $(\ref{eq:1})$, ta có:
\[\begin{align} f(x_n) &\leq f(x^*)+\nabla f(x_{n-1})^T(x_{n-1} - x^*) - \dfrac{\alpha}{2}\|\nabla f(x_{n-1})\|_2^2\nonumber\\ &=f(x^*) + \dfrac{1}{2\alpha}\left(2\alpha\nabla f(x_{n-1})^T(x_{n-1} - x^*) - \alpha^2\|\nabla f(x_{n-1})\|_2^2\right)\nonumber\\ &=f(x^*) + \dfrac{1}{2\alpha}(\|x_{n-1} - x^*\|_2^2 - \|x_{n-1} - x^* - \alpha\nabla f(x_{n-1})\|_2^2)\nonumber\\ &=f(x^*) + \dfrac{1}{2\alpha}(\|x_{n-1} - x^*\|_2^2 - \|x_n - x^*\|_2^2)\nonumber\\ \Leftrightarrow &f(x_n) - f(x^*)\leq\dfrac{1}{2\alpha}(\|x_{n-1} - x^*\|_2^2 - \|x_n - x^*\|_2^2)\nonumber \end{align}\]Từ đây, ta có được
\[\sum_{i=1}^nf(x_i) - f(x^*)\leq\dfrac{1}{2\alpha}(\|x_0 - x^*\|_2^2 - \|x_n - x^*\|_2^2)\]Vì $f(x_i)$ giảm khi i tăng nên $n(f(x_n) - f(x^*))\leq\dfrac{1}{2\alpha}(||x_0 - x^*||_2^2 - ||x_n - x^*||_2^2)\leq\dfrac{1}{2\alpha}||x_0 - x^*||_2^2$ hay $f(x_n) - f(x^*)\leq\dfrac{||x_0 - x^*||_2^2}{2n\alpha}$. Từ đây, ta có được điều phải chứng minh. Như vậy, trong trường hợp trung bình, thuật toán Gradient Descent có tốc độ hội tụ $\mathcal{O}\left(\dfrac{1}{n}\right)$ với $\alpha\leq\dfrac{1}{L}$. Tuy tốc độ này không nhanh bằng việc sử dụng phương pháp Newton-Raphson (hội tụ bậc 2), thuật toán Gradient Descent ổn định hơn do chỉ tính đạo hàm một lần và vẫn đảm bảo tốc độ hội tụ ở ngưỡng chấp nhận được.
Kết luận
Thuật toán Gradient Descent nhìn chung là một thuật toán ổn định với sự đảm bảo trong việc tìm ra nghiệm tối ưu sau một số lượng vòng lặp đủ lớn. Ý tưởng của thuật toán Gradient Descent cũng rất đơn giản trực tiếp nhưng vẫn có thể đánh bại các thuật toán tối ưu hoá lâu đời. Điều đáng tiếc là thuật toán Gradient Descent có tốc độ hội tụ chậm hơn các phương pháp lâu đời khác và việc phải lựa chọn tốc độ học sao cho phù hợp đôi khi đòi hỏi sự dày công thử nghiệm (việc tính hệ số Lipschitz cũng đòi hỏi độ phức tạp khá lớn). Chính vì vậy, nhiều phiên bản cải tiến hơn của Gradient Descent đã ra đời nhưng đó là chủ đề cho các bài viết tiếp theo.
