1. Giới thiệu
Trong bài viết trước, mình đã giới thiệu về hai thuật toán Policy Iteration và thuật toán Value Iteration trong việc giải các bài toán mà các đặc tính của môi trường đã được biết sẵn (cụ thể là mô hình Markov của môi trường đã được tìm ra từ trước khi thuật toán được thực thi). Trong bài viết này, mình sẽ viết về trường hợp mà bạn không biết được hết toàn bộ đặc tính của môi trường và cách hiệu quả nhất để có thể thu thập dữ liệu đó chính là tương tác và cải thiện policy dựa trên phản hồi.
2. Phát biểu bài toán
Bài toán RL trong trường hợp môi trường không được biết trước toàn bộ hiện đang là một trong những bài toán nhức nhối trong giới RL. Bài toán được phát biểu như sau:
Cho một môi trường $E$ có $\mathcal{S}$ là tập hợp các state và $\mathcal{A}$ là tập hợp các tương tác có thể giữa agent và $E$. Các state thuộc $\mathcal{S}$ có thể chuyển đổi qua lại lẫn nhau dưới một mô hình xác suất mà agent không hề được biết trước. Tìm một policy $\pi$ sao cho hàm value $V^\pi(s)$ đạt giá trị lớn nhất với mọi $s$.
Qua phát biểu của bài toán, có thể thấy cách duy nhất để một agent có thể cải thiện policy của mình đó là thông qua việc tổng hợp các phản hồi của môi trường lại và đưa qua quyết định tốt nhất (hàm $\pi$ cực đại hoá hàm $V^\pi$). Vấn đề lại nằm ở chỗ làm thế nào để từ một lượng lớn phản hồi của môi trường có thể đưa ra policy tốt nhất. Quay lại thuật toán Value Iteration, nếu bạn để ý, việc chọn hành động a sao cho hàm $\pi(s) = \arg\max_a Q^\pi (s, a)$ có khả năng giúp thuật toán hội tụ mặc dù chậm. Nên bài toán trở nên vô cùng đơn giản từ việc tìm ra policy $\pi$ sao cho $V^\pi$ đạt giá trị lớn nhất với mọi s thành bài toán ước lượng $Q^\pi (s, a)$ với mọi cặp $(s, a)$ cho trước policy $\pi$, rồi sau đó lấy action $a$ sao cho $Q^\pi (s, a)$ và gán nó thành giá trị của $\pi (s)$. Tuy nhiên, làm sao để ước lượng hàm $Q^\pi (s, a)$? Nếu bạn là một học sinh/sinh viên có kiến thức nền về Xác suất, chắc các bạn biết đến phương pháp cực nổi tiếng sau.
3. Phương pháp xấp xỉ Monte-Carlo và ứng dụng trong việc giải các bài toán RL không biết trước môi trường
Chính xác! Không ai khác ngoài nhà toán học nổi tiếng Monte-Carlo. Cho những ai không biết về phương pháp này, sau đây mình sẽ cho một ví dụ. Giả sử bạn muốn biết rằng đồng xu bạn đang cầm có xác suất ra mặt sấp hay ngửa là bao nhiêu. Các bạn sẽ trả lời $50\%$. Nhưng các nhà Toán học và Vật lí học đã chứng minh đồng xu cân bằng là không tồn tại. Từ đó có thể thấy chắc chắn xác suất không thể nào là $50\%$. Thế làm sao bây giờ nhỉ? Vậy thì cứ tung đồng xu lên thôi! Tung đồng xu N lần rồi tính số lần ra mặt ngửa (gọi nó là $M$). Như vậy, xác suất để đồng xu ra mặt ngửa sẽ xấp xỉ bằng $M/N$ nếu $N$ là một số cực lớn (theo qui luật số lớn). Đây chính là tư tưởng của phương pháp Monte-Carlo: để ước lượng một tham số $\theta$, một trong những cách đơn giản nhanh chóng là lấy thật nhiều mẫu từ phân phối của $\theta$ và tính trung bình mẫu là được xấp xỉ gần bằng với $\theta$.
Như vậy, nếu áp dụng vào giải bài toán RL không rõ môi trường, chỉ cần chú ý rằng $Q^\pi {s, a} = \mathbb{E}[r_t + \gamma r_{t+1} + \ldots | s_t = s, a_t = a]$. Như vậy thì việc đơn giản nhất là đầu tiên tạo ra một policy ngẫu nhiên rồi lấy thật nhiều chuỗi state, reward và ước lượng $Q$ bằng trung bình mẫu rồi lấy $\arg\max$ là xong. Tư tưởng sẽ được mô tả căn bản bởi mã giả dưới đây:

Lưu ý rằng, dòng 3 của vòng for được rút ra bằng quan sát sau: nếu đặt $\widehat{a}_t = \frac{a_1 + a_2 + \ldots + a_t}{t}$ thì $\widehat{a}_t = \frac{1}{t}a_t + \frac{t-1}{t}\widehat{a}_{t-1} = \widehat{a}_{t-1} + \frac{1}{t}(a_t - \widehat{a}_{t-1})$. Tuy nhiên, có một vấn đề: giả sử agent ở state $s$ và trước mặt là tường, policy ứng với s được khởi tạo là đi về trước. Thế thuật toán đó có cải thiện gì ở policy không? Tất nhiên là không. Đây chính là vấn đề khám phá và khai thác trong các bài toán RL (exploration và exploitation). Nếu agent của bạn không chịu khám phá mà chỉ biết khai thác policy hiện có thì có một vấn đề nghiêm trọng đó là nếu policy hiện có đã tệ rồi thì nó sẽ chẳng cải thiện gì thêm (trường hợp trước, do policy khởi tạo đã là đâm đầu vào tường, lấy mẫu của state đó là một việc vô ích). Vậy nên có một cách có thể tận dụng để có thể cải thiện thuật toán này đó chính là sử dụng thuật toán đó chính là giới thiệu một chút random vào trong thuật toán bắt agent phải khai thác policy cũ với xác suất $1 - \epsilon$ và chọn random bất kì action nào trong $\mathcal{A}$ với xác suất $\epsilon$. Thuật toán này gọi là $\epsilon$-greedy Monte-Carlo. Mã giả của thuật toán được mô tả như hình dưới:

Thuật toán trên sẽ hội tụ về policy tối ưu nếu và chỉ nếu nó thoả mãn điều kiện GLIE (viết tắt cho Greedy Limit of Infinite Exploration). Điều kiện này phát biểu như sau: một thuật toán RL được gọi là GLIE nếu và chỉ nếu thoả mãn 2 điều kiện sau:
- Các cặp $(s, a)$ được đếm vô số lần hay $N(s,a)\to\infty$ khi $i\to\infty$ (i là số vòng lặp của thuật toán).
- $\lim_{i\to\infty}\pi(a|s) = \arg\max_a Q(s, a)$.
Một trong những cách đơn giản nhất là xây dựng chuỗi $\epsilon_i=\frac{1}{i}$ với $i$ là số vòng lặp. Qua đó, thuật toán sẽ vừa thăm dò các cặp $(s, a)$ vô số lần (do có yếu tố random) vừa hội tụ được policy (do mức độ khai thác sẽ tăng theo thời gian, còn mức độ khai phá sẽ giảm). Nhìn chung thì thuật toán này đã giải quyết được vấn đề không khai phá của thuật toán Monte-Carlo thuần nhưng nó lại không thoát khỏi việc là một thuật toán random. Trong trường hợp agent đã khám phá một policy là tệ, việc random sẽ không hề đảm bảo rằng agent sẽ không đi lại nước đi đó nữa. Chúng ta cần một thuật toán có thể bằng một cách nào đó tận dụng dữ liệu một cách hiệu quả không chỉ lấy mẫu một cách random.
Bootstrapping: Học từ kinh nghiệm trong quá khứ
Chúng ta hãy cùng quan sát lại thuật toán Value Iteration một chút

Như các bạn có thể thấy, thuật toán Value Iteration hội tụ chính là nhờ vào việc sử dụng toán tử contraction kết hợp với các giá trị value của các iteration trước (một toán tử $O$ được gọi là contraction nếu và chỉ nếu $|O(V’) - O(V)| < |V’ - V|$, nếu các bạn đọc phần Phụ lục của bài viết trước sẽ thấy điều này). Nói một cách khác, thuật toán Value Iteration hội tụ là do nó đã sử dụng các giá trị value từ vòng lặp trước để cải thiện hàm value ở vòng lặp sau. Việc sử dụng giá trị phía trước để tính các giá trị đằng sau đó được gọi là bootstrapping. Rõ ràng, bootstrapping cũng đóng vai trò quan trọng trong Policy Iteration (bạn phải bootstrap hàm value trước rồi mới tính được hàm $Q$ sau đó mới cải thiện được policy).
Như vậy, có cách nào để vừa sampling (như Monte-Carlo) mà vừa bootstrapping (như các thuật toán trong bài viết trước) không? Đây chính là tư tưởng chính của hai thuật toán SARSA và Q-Learning nổi tiếng.
SARSA - State Action Reward State Action
Cách đầu tiên là bạn lấy mẫu state sau và bootstrap giá trị $Q^\pi$ của state sau và action ứng với state sau theo policy $\pi$. Mã giả của thuật toán được mô tả ở hình dưới đây:

So sánh với thuật toán $\epsilon$-greedy Monte-Carlo, thuật toán SARSA đã thay hệ số $\frac{1}{N(s,a)}$ bằng $\alpha$ và thay biến $G$ bằng biểu thức $r_t + \gamma Q^\pi(s_{i+1}, a_{i+1})$. Hằng số $\alpha$ lúc này đã có một cái tên khác cực kì thân thuộc với các thuật toán khác trong họ Máy học, tốc độ học hay learning rate. Và rõ ràng, hành động tính $r_t + \gamma Q^\pi(s_{i+1}, a_{i+1})$ chính là hành động bootstrap giá trị $Q$ của cặp $(s, a)$ kế tiếp theo policy $\pi$. Việc chứng minh trực tiếp hội tụ của thuật toán này hiện chưa có (theo bài báo này) nhưng nó được công nhận không chứng minh rằng nếu thuật toán SARSA thoả GLIE và tốc độ học $\alpha_i$ thoả mãn điều kiện Robbins-Munro ($\sum_{i=1}^\infty\alpha_i = \infty$ và $\sum_{i=1}^\infty\alpha_i^2 < \infty$) thì thuật toán hội tụ (dãy $\alpha_i = \frac{1}{i}$ là một dãy thoả mãn điều kiện này). Có một điều mình muốn nhắc (vì đây là khái niệm mình mới bị cô hỏi mà lóng ngóng) đó là hai khái niệm thuật toán on-policy và thuật toán off-policy. Các thuật toán policy luôn khởi tạo một policy ban đầu và cố gắng cải thiện policy bằng cách đi theo thuật toán đó. Các thuật toán off-policy lại cố gắng cải thiện policy của mình bằng cách đề xuất ra một policy khác, so sánh giữa policy hiện tại và policy thay thế và thay đổi policy tuỳ vào ngữ cảnh của agent. Một ví dụ của thuật toán on-policy chính là thuật toán SARSA. Thuật toán SARSA học bằng cách men theo “hướng” của policy đầu để có thể cải thiện policy của mình. Chính vì vậy, việc khởi tạo policy là một việc cực kì nhức đầu với thuật toán này vì nếu khởi tạo sai thì bạn sẽ hội tụ đến policy rất là tệ (có nhiều dao động và thậm chí là dao động mạnh). Tuy nhiên, theo định nghĩa, các bạn có thể thấy Value Iteration và Policy Iteration là hai thuật toán off-policy. Vậy liệu có thuật toán off-policy nào vừa sampling vừa bootstrapping không? Câu trả lời nằm ở phần dưới đây.
Thuật toán Q-Learning
Thuật toán Q-Learning kế thừa thuật toán SARSA nhưng có một chút biến đổi: chiến thuật của nó lần này là bootstrap hành động có giá trị $Q$ lớn nhất thay vì chỉ bootstrap hành động ứng với state kế tiếp. Mã giả của thuật toán được mô tả như hình dưới:

Như mình đã đề cập, thuật toán này bootstrap hành động có giá trị $Q$ lớn nhất bằng cách sử dụng biểu thức $r_t + \gamma \max_a Q^\pi (s_{t+1},a)$. Điều này cũng có nghĩa thuật toán Q-Learning sẽ có một policy thay thế (vì hành động của state kế tiếp có khả năng sẽ bị thay đổi do lấy max). Do đó, Q-Learning là một thuật toán off-policy. Thuật toán Q-Learning cũng có tốc độ hội tụ phụ thuộc vào việc khởi tạo policy ban đầu nhưng nó không quá nặng bằng SARSA do Q-Learning có khả năng đề ra policy thay thế để cải thiện mô hình cũ. Thuật toán Q-Learning có hai mức độ hội tụ. Nếu chỉ quan tâm đến việc tìm được giá trị $Q$ tối ưu thì chỉ cần thuật toán phải đi qua mỗi cặp $(s, a)$ vô số lần và $\alpha_t$ phải thoả điều kiện Robbins-Munro. Tuy nhiên, nếu muốn hội tụ tối ưu thì thuật toán này phải là GLIE và điều kiện Robbins-Munro phải được thoả mãn.
Thí nghiệm thực tế trên hai thuật toán
Vâng, đây là quá trình khổ sở nhất các bạn ạ (vì việc khởi tạo ảnh hưởng lớn đến độ hội tụ của hai thuật toán nên mình phải chạy đi chạy lại khá nhiều lần, mỗi lần 8 tiếng). Trước khi bước vào kết quả, mình xin mô tả môi trường của mình một chút. Lần này mình sử dụng môi trường mê cung ở đây. Môi trường có dạng như sau:
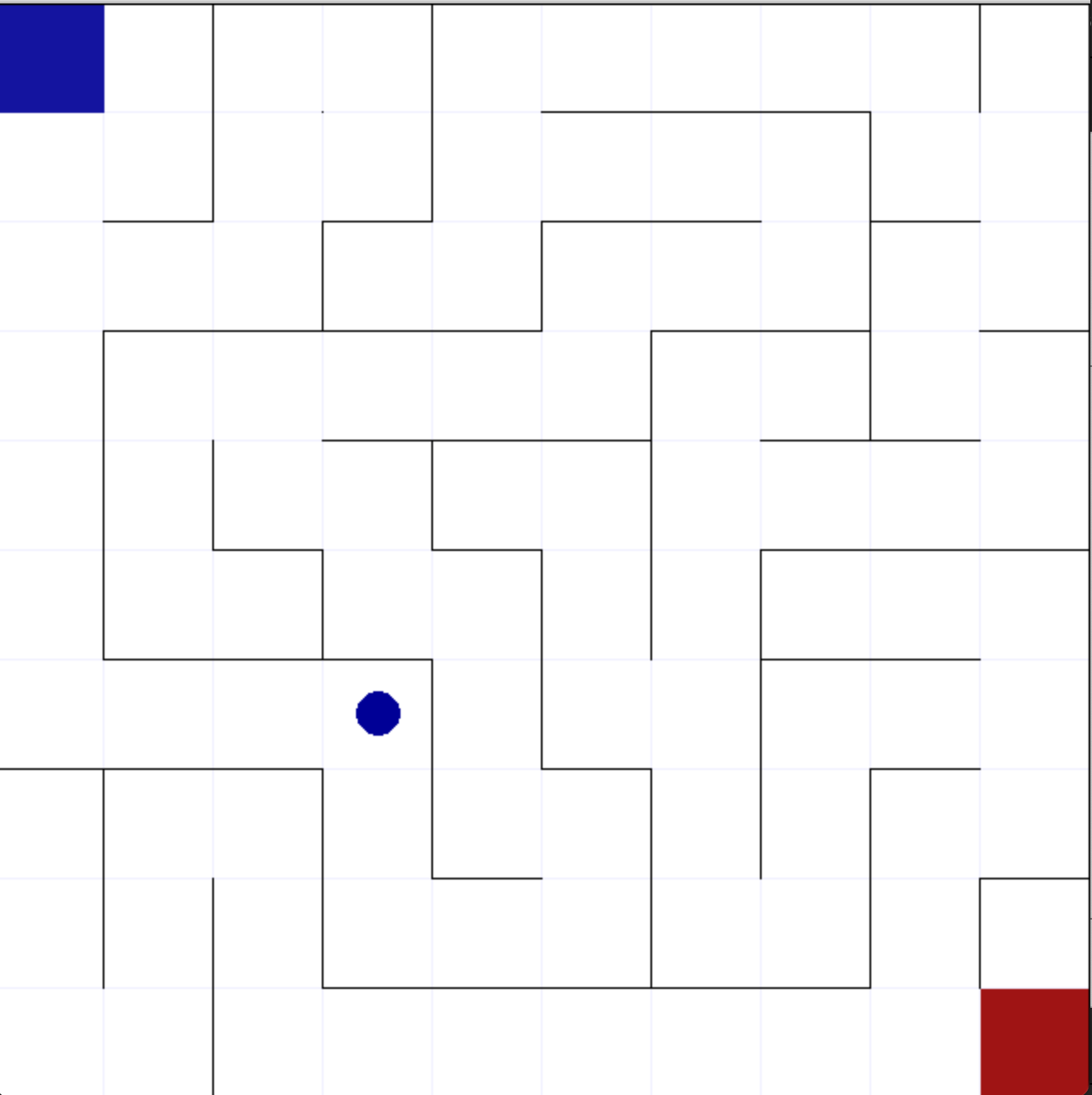
Trong hình trên, ô vuông xanh ở góc trên bên trái mê cung là ô vuông bắt đầu, ô vuông bên dưới góc phải màu đỏ là ô kết thúc, chấm tròn màu xanh chính là agent, các cạnh màu đen đậm là tường. Tại vị trí $(i, j)$, khi agent thực hiện action $a$ có hai khả năng xảy ra: nếu hành động $a$ không đụng tường thì hành động $a$ được thực thi, vị trí mới và reward mới được trả về; nếu hành động $a$ đụng tường, vị trí $(i, j)$ được trả về và reward hiện tại ở vị trí $(i, j)$ sẽ được trả về. Hàm reward của mình sẽ được định nghĩa là $-\frac{0.01}{n}$ với $n$ là số step đã đi được. Điều này sẽ làm cản trở việc agent đi đường cực dài để đến ô đỏ. Ngoài ra việc sử dụng phép chia sẽ làm cản trở việc agent chỉ đi chung quanh vị trí bắt đầu mà vẫn có reward.
Và đây là kết quả của mình:
Thuật toán SARSA:
Thuật toán SARSA mình gặp rất nhiều vận may vì chỉ cần 2 lần chạy mình đã có agent hội tụ chỉ sau 125 vòng lặp (như trên video mình up trên youtube). Điều thú vị là thuật toán này lại bỏ đi việc khai phá rất nhanh và tập trung vào khai thác policy hiện hành (chắc do mình ăn hên được policy đầu tốt).
Thuật toán Q-Learning:
Thuật toán Q-Learning mình gặp xui nhiều nhất. Mình đã chạy tổng cộng 5 lần nhưng chỉ có đúng một lần là thuật toán này hội tụ sau 5000 vòng lặp với performance xấp xỉ bằng performance của SARSA (vì ở cuối Q-Learning agent tốn 3s để đi từ xanh đến đỏ còn SARSA chỉ tốn 2s).
Kết luận
Vậy khi nào bạn nên sử dụng thuật toán nào? Theo mình đọc trên mạng, thuật toán SARSA được sử dụng khi bạn quan tâm đến performance của agent. Ví dụ trong trường hợp bạn làm một con robot vệ sinh nhà cửa, chẳng may nó té cầu thang thì phải mua con robot khác train tiếp (và một con robot khá là đắt). Việc sử dụng thuật toán SARSA có khả năng sẽ giúp bạn hạn chế điều này vì robot chỉ đi theo policy được khởi tạo ban đầu và dần cải thiện. Thuật toán Q-Learning sử dụng khi bạn chả cần quan tâm đến agent hoạt động thế nào mà chỉ muốn có được policy tối ưu, thường được thấy rất nhiều trong việc train AI để chơi game. Trong bài viết tới, mình sẽ cố gắng viết về việc sử dụng Deep Learning trong các bài toán không biết trước được môi trường.
